Population Dynamics: Predator-Prey Interactions
 Objective
Objective
The purpose of this exercise is to develop an understanding of population dynamics by modeling the dynamics of a hypothetical population. After we have established basic population dynamic relationships, you will investigate these relationships in greater detail by exploring the population dynamics of a hypothetical predator - prey population of foxes and rabbits.
Figure 1
Fox predator catching a prey rabbit
An effective means of understanding such a system is to model it, i.e. to think about the system critically, identifying stocks, flows, converters and connectors, and create a conceptual diagram. You will be given a description of the system, and some initial parameters. You will then develop a conceptual diagram together in groups. This diagram will serve to summarize our knowledge of the system, and convert descriptive information into symbols that are easy to manipulate. From the conceptual diagram, the descriptive data, and some initial parameters, you will construct a STELLA model that describes the rabbit-fox population dynamics.
Population Dynamics
In this lab we will be considering foxes and rabbits. We need to first examine the basics of population dynamics using the rabbit population to examine how populations change over time. Start up STELLA and click on the modeling tab.
The first stock ![]() in our
model is Rabbit Population.
in our
model is Rabbit Population.
Recall that changes in stocks are modeled with the flow tool: ![]() .
Changes in population are caused by Rabbit Births, so add it to your model.
.
Changes in population are caused by Rabbit Births, so add it to your model.
The final piece needed for a complete model is the Rabbit
Birth Rate. Add this using the converter
tool: ![]() .
Assume that the rabbit birth rate is 4% per day or .04 and your population
starts with 10 rabbits.
.
Assume that the rabbit birth rate is 4% per day or .04 and your population
starts with 10 rabbits.
Use the connector tool: ![]() to complete the connections in your population model.
to complete the connections in your population model.
Define births with the following equation (this is the equation for our exponential growth model):
Rabbit Births = Rabbit Birth Rate * Rabbit Population
SAVE your model.
Specify an amount of time for the model under length of simulation:
From = 0, to = 250, DT = 1, and Unit of Time = days. Click OK.
Set up the viewing graph with the graph icon ![]() .
Define your graph with the Rabbit Population stock. Run the model.
.
Define your graph with the Rabbit Population stock. Run the model.
The graph that appears should look like Figure 2.
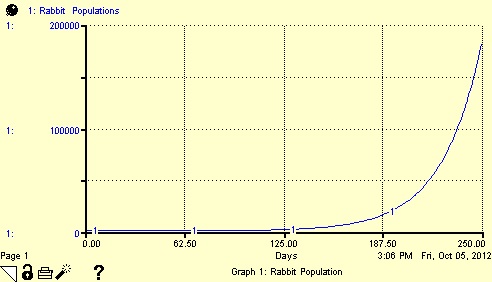
Figure 2
Graph of exponential population growth
A More Realistic Model
The model we have created works well, but recall that all populations have limits to their growth. How can we fix the model to give a more realistic result? We can show this effect in our model by adding a carrying capacity variable and changing the equation for Rabbit Births.
Carrying capacity is the maximum size a population can grow to given the available resources.
Add a converter to the model, below and to the right of the flow icon, and name it Carrying Capacity. Connect it to Rabbit Births. What would be a good value for carrying capacity for your population?
Change your equation to include the carrying capacity component of your model (this is our equation for the logistic growth model).
Rabbit Births = Rabbit Birth Rate * Rabbit Population * (1 - (Rabbit Population / Carrying Capacity))
The model should now look like Figure 3.
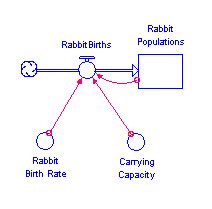
Figure 3
Population model with carrying capacity
Run the model with the same time specs. The new graph should look like Figure 4.
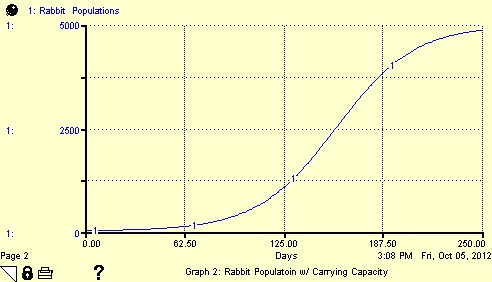
Figure 4
Graph of population with carrying capacity
Judging by the graph, this model seems to be more in line with the way a population might increase in an environment with finite resources.
Question 1
Describe two factors that would change carrying capacity in nature.
Rabbits and Foxes
Save the first part of this model. Now we will incorporate a predator into the system. First we have to describe how the prey (rabbit) population changes and then describe how the predator (fox) population subsequently changes, since the predator is dependent on the prey species for growth and survival. Below is a written description of how this system works as well as some data on the rates of the processes. Read through this information.
- For now, neither population has a carrying capacity (i.e. delete the carrying capacity converter).
- The rabbit population tends to exhibit exponential growth unless it is held in check by a predator. Use your original rabbit model, but delete (blow up) the Carrying Capacity converter.
- Rabbit mortality is determined entirely by fox predation.
- Foxes eat rabbits at a rate proportional to the number of encounters between foxes and rabbits.
- Fox population growth rate is determined by the amount of rabbits they eat (foxes tend to reproduce faster if they are well fed) and their physiological efficiency of converting energy gained by ingestion of prey to reproduction (simply put: the efficiency of converting eaten rabbits into new baby foxes).
- Natural death processes determine Fox mortality.
- Also at your disposal are data describing the rates at which these processes occur. Normally, researchers would determine these rates in the field or experimentally.
- The growth rate of the rabbit population in the absence of predation is 4% / day (0.04).
- The foxes' physiological efficiency of converting ingested rabbits to new offspring is 3% (0.03).
- The natural death rate of foxes is 4% (0.04) / day.
- The probability of a fox meeting a rabbit is 0.05% (.0005) / day.
Then, in a small group, draw on a piece of paper a conceptual diagram on these data.
This diagram allows you to see, using symbols, how parts of the model relate to one another. It is the intermediate step in understanding the dynamics and should serve as the template for your STELLA model.
You should have an idea of what the outcome should be. In other words, how do you think the fox population should grow in relation to the rabbit population? Sketch out a quick graph of your expectations and ask yourself "why should it look this way and how might it look different?" This should help you figure out whether or not the model is functioning well once you run it in Stella. Show your GSI your diagram and get approval before opening Stella.
Troubleshoot and Revise
Here are some tips to help exterminate the bugs in your model:
- Make sure that there are no typos in your model. You should not type in any variable names when defining flows; instead select them from the list on the left box.
- Note that you cannot have the same name for two different components of the model.
- Are your parentheses correct and balanced?
- If you can't enter formulas, are you in modeling mode?
- Make sure that you have the flows going in the correct direction.
- Make sure the connectors between the icons exist and are connected to the correct icons.
- No graph appears when running? Have you defined the graph? Do you need to manually set the scale of the Y-axis so that the curves are scaled properly?
- Test and revise the model until it is running correctly.
Questions
(Question 1 (1 point) is located above)
Question 2 (2 points)
Write the prediction that you created prior to running this model about the population dynamics of foxes and rabbits. Next, describe the dynamics of both
populations under the conditions outlined above and discuss why this pattern
occurs and compare your results with your prediction. Submit a copy of the model, the equations and a graph of the run.
Question 3 (2 points)
What parameter value(s) would you change to have the fox population crash (go to zero), and the rabbit population survive? Test your prediction and include your graph in your submission.
Question 4 (2 points)
What parameter value(s) would you change to have the rabbit population crash? How would this affect the fox population? Test your prediction and include your graph in your submission.
Question 5 (3 points)
What would you expect to happen (in terms of the dynamics of both populations) if rabbits exhibited logistic (s-shaped) growth? Test this out by modifying your model and adding this feature to the rabbit population. First, reintroduce the carrying capacity function (remember to change your rabbit birth rate equation to the logisitc growth equation). Now, set the carrying capacity to 10000. Explain the dynamics and include a graph.
Now, let's explore the impact of a long drought where the rabbit carrying capacity is much lower. Reduce the carrying capacity to 5000 from day 250 onwards. Explain the impact of a long drought on the rabbit population. Include a graph of this simulation in your submission.
For Next Week, turn in:
- Completed Stella Model (.STM file)
- Word doc containing:
- Answers for Q1-5 and…
- 5 Graphs
- (1) Exponential Rabbit/Fox Interaction
- (1) Crashing fox population, rabbits win!
- (1) Crashing rabbit population, who wins?
- (2) Carrying capacity at 10,000 and one with reducing carrying capacity as a graphical function.
Sources
http://www.canids.org/SPPACCTS/redfox.htm